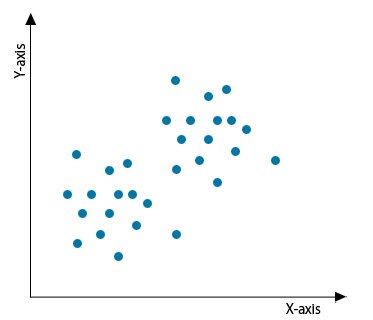
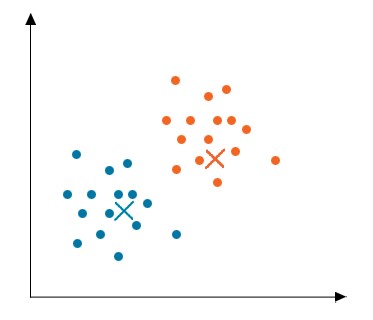
دستهبندی نشده
مقدمهای بر الگوریتم خوشهبندی کی k-means
الگوریتم خوشهبندی k-میانگین به عنوان یک روش یادگیری بدون نظارت تعریف میشود که دارای یک فرآیند تکراری است که در آن مجموعه دادهها در k تعداد خوشهها یا زیرگروههای از پیش تعریفشده بدون عضو مشرک گروهبندی میشوند و نقاط داخلی خوشه را تا حد ممکن شبیه به هم میسازند و در عین حال تلاش میکنند تا خوشهها در فضایی مجزا، نقاط داده را به یک خوشه اختصاص دهد به طوری که مجموع فاصله مجذور بین مرکز خوشه و نقطه داده در کمینه باشد، در این حالت مرکز ثقل خوشه میانگین حسابی نقاط دادهای است که در خوشه قرار دارند.
آشنایی با الگوریتم خوشه بندی k _ میانگین
این الگوریتم یک الگوریتم تکراری است که مجموعه داده را با توجه به ویژگیهای آنها به تعداد k از خوشهها یا زیرگروههای متمایز از پیش تعریفشدهای که عضو مشترکی ندارند تقسیم میکند. نقاط داده بین خوشهها را تا حد امکان مشابه میکند و همچنین سعی میکند تا آنجا که ممکن است خوشهها را حفظ کند. اگر مجموع فاصله مجذور بین مرکز خوشه و نقاط داده در کمینه باشد، نقاط داده را به یک خوشه اختصاص میدهد، جایی که مرکز خوشه میانگین حسابی نقاط دادهای است که در خوشه هستند. تغییرات کمتر در خوشه منجر به نقاط داده مشابه یا همگن در داخل خوشه میشود.
الگوریتم خوشهبندی کی-میانگین چگونه کار میکند؟
الگوریتم خوشهبندی k-means به ورودیهای زیر نیاز دارد:
= K تعداد زیر گروهها یا خوشهها
مجموعه نمونه یا آموزشی: {x1, x2, x3,………xn}
حال فرض کنیم مجموعه دادهای داریم که برچسب ندارد و باید آن را بین خوشهها تقسیم کنیم.
حالا باید تعداد خوشهها را پیدا کنیم.
این کار با دو روش قابل انجام است:
- روش آرنج
- روش هدف
1.روش آرنج
در این روش، منحنی بین “در مجموع مجذورها” (WSS) و تعداد خوشهها رسم میشود. منحنی ترسیم شده شبیه بازوی انسان است. این روش را روش آرنج مینامند زیرا نقطه آرنج در منحنی تعداد بهینه خوشهها را به ما میدهد. در نمودار یا منحنی، بعد از نقطه آرنج، مقدار در مجموع مجذورها بسیار آهسته تغییر میکند، بنابراین باید نقطه آرنج را در نظر گرفت تا مقدار نهایی تعداد خوشهها را به دست آورد.
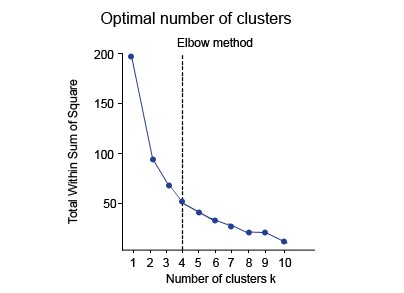
-
بر اساس هدف مورد نظر
در این روش دادهها بر اساس معیارهای مختلف تقسیم میشوند و پس از آن مشخص میشود که برای آن مورد چقدر خوب عمل کرده است. به عنوان مثال، چیدمان پیراهنها در بخش پوشاک مردانه در یک مرکز خرید بر اساس معیار سایز انجام میشود. این کار بر اساس قیمت و برندها نیز قابل انجام است. بهترین گزینه برای ارائه تعداد بهینه خوشهها، یعنی مقدار K انتخاب، میشود.
اکنون بیایید به مجموعه دادههای داده شده در بالا برگردیم. ما میتوانیم تعداد خوشهها، یعنی مقدار K را با استفاده از هر یک از روشهای بالا محاسبه کنیم.
چگونه از روشهای فوق استفاده کنیم؟
حالا بیایید روند اجرا را ببینیم:
مرحله 1: مقداردهی اولیه
ابتدا مقدار اولیه هر نقطه تصادفی به نام مرکز خوشه را مشخص کنید. هنگام شروع اولیه، باید مراقب باشید که مرکزهای خوشه باید کمتر از تعداد نقاط داده آموزشی باشد. این الگوریتم یک الگوریتم تکراری است. از این رو دو مرحله بعدی به صورت تکراری انجام میشود.
مرحله 2: وظیفه خوشه
پس از مقداردهی اولیه، با عبور عرضی نقاط داده، فاصله بین تمام مرکزها و نقاط داده محاسبه میشود. اکنون خوشهها بسته به حداقل فاصله از مرکزها تشکیل میشوند. در این مثال دادهها به دو خوشه تقسیم میشوند.
مرحله 3: حرکت دهی مرکز
از آنجایی که خوشههای تشکیل شده در مرحله بالا بهینه نیستند، بنابراین باید خوشههای بهینه سازی شده را تشکیل دهیم. برای این کار، ما باید مرکزها را به طور مکرر به یک مکان جدید منتقل کنیم. نقاط داده یک خوشه را بگیرید، میانگین آنها را محاسبه کنید و سپس مرکز آن خوشه را به این مکان جدید منتقل کنید. همین مرحله را برای همه خوشههای دیگر تکرار کنید.
مرحله 4: بهینه سازی
دو مرحله فوق به صورت مکرر انجام میشود تا زمانی که مرکزها از حرکت باز میایستند، یعنی دیگر موقعیت خود را تغییر نمیدهند و ساکن میشوند. هنگامی که این کار انجام شد، الگوریتم کی میانگین همگرا نامیده میشود.
مرحله 5: همگرایی
اکنون، این الگوریتم همگرا شده است و خوشههای متمایز تشکیل شده و به وضوح قابل مشاهده میباشند. این الگوریتم بسته به نحوه مقدار اولیه خوشهها در مرحله اول میتواند نتایج متفاوتی به دست آورد.
کاربردهای الگوریتم خوشه بندی کی میانگین
در زیر لیست یک سری از کاربردها نمایش داده شده است:
- بخش بندی بازار
- خوشه بندی اسناد
- تقسیم بندی تصویر
- فشرده سازی تصویر
- چندی سازی برداری
- آنالیز خوشهای
- یادگیری ویژگی یا یادگیری فرهنگ لغت
- شناسایی مناطق جرم خیز
- کشف تقلب در بیمه
- تجزیه و تحلیل دادههای حمل و نقل عمومی
- خوشه بندی داراییهای فناوری اطلاعات
- تقسیم بندی مشتریان
- شناسایی دادههای سرطانی
- در موتورهای جستجو استفاده میشود
- پیشبینی میزان مصرف مواد مخدر
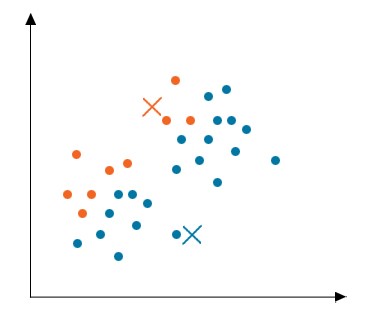
مزایای الگوریتم خوشهبندی کی میانگین
در زیربه تعدادی از مزایای k-means اشاره شده است:
- سریع
- قدرتمند
- قابل فهم
- نسبتا کارآمد
- اگر مجموعه دادهها متمایز باشند، بهترین نتایج را میدهد.
- خوشههای با دوام بالاتولید کنید.
- هنگامی که مرکزها دوباره محاسبه میشوند، خوشه تغییر میکند.
- قابل انعطاف
- آسان برای تفسیر
- هزینه محاسباتی مناسبتر
- افزایش دقت
- با خوشههای کروی بهتر کار میکند.
معایب الگوریتم خوشهبندی کی میانگین
در زیر معایب الگوریتم ذکر شده است:
- برای تعداد مراکز خوشه نیاز به مشخصات قبلی دارد.
- اگر دو داده به شدت همپوشانی داشته باشند، تشخیص آنها سخت و نمیتوان گفت که دو خوشه وجود دارد.
- با بازنماییهای مختلف دادهها، نتایج به دست آمده نیز متفاوت است.
- فاصله اقلیدسی می تواند عوامل را به طور نابرابر وزن کند.
- بهینه محلی تابع، خطای مجذور میدهد.
- گاهی اوقات انتخاب مراکز به طور تصادفی نمیتواند نتایج مثمر ثمری داشته باشد.
- فقط در صورتی میتوان از آن استفاده کرد که معنی آن تعریف شده باشد.
- نمی تواند دادههای پرت و نویزدار را مدیریت کند.
- برای مجموعه دادههای غیر خطی قابل استفاده نیست.
- ناسازگار است.
- حساس به مقیاس
- اگر با مجموعه دادههای بسیار بزرگ مواجه شوید، ممکن است کامپیوتر از کار بیفتد.
- ناتوان در پیشبینی بدون مشکل

مترجم:
Diba Zabeti Targhi