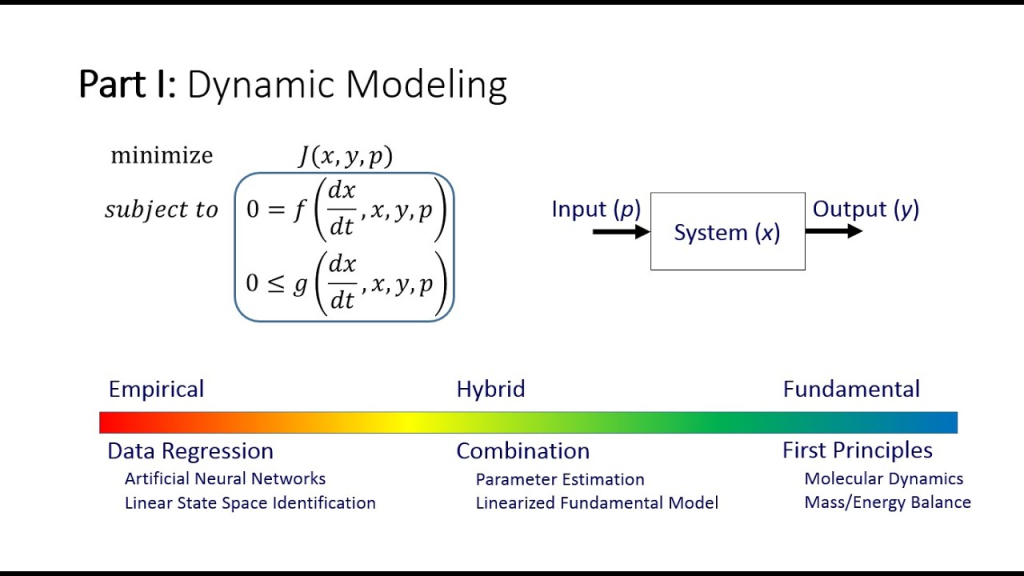
مدلسازی دینامیکی و کینتیک آنزیمی

درباره مدلسازی دینامیکی و کینتیک آنزیمی

مدل‌سازی ریاضی یک فرآیند کلیدی برای توصیف رفتار شبکه‌های بیولوژیکی است. یکی از سخت‌ترین چالش‌ها، ساخت مدل‌هایی است که امکان پیش‌بینی کمی وضعیت سلول‌ها را در طول زمان فراهم می‌کند. اخیراً، این موضوع از طریق رویکردهای جدید در کامپیوتر، مانند مدلسازی دینامیکی، کینتیک آنزیمی، استفاده از روش‌های پیش‌بینی فنوتیپ، و طراحی مسیر از طریق الگوریتم‌های بهینه‌سازی، شروع شده است.

آنزیم‌ها کاتالیزورهای بیولوژیکی هستند که برای افزایش سرعت واکنش عمل می‌کنند بدون اینکه خودشان مصرف شوند یا تغییر کنند. آنها مخصوص یک نوع واکنش و یک یا تعداد کمی از واکنش‌دهنده‌های نزدیک به هم هستند که به عنوان سوبسترا شناخته می‌شوند. آنزیم‌ها جزء حیاتی سلول هستند، زیرا بدون آنها، بسیاری از واکنش‌های بیولوژیکی برای حفظ حیات بسیار کند خواهند بود.

کینتیک آنزیمی مطالعه سرعت واکنش‌های آنزیمی و شرایطی است که بر آنها تأثیر می‌گذارد. آنزیم‌ها یک مسیر جایگزین برای واکنش فراهم می‌کنند که انرژی فعال‌سازی کمتری (Ea) دارد – حداقل انرژی ورودی مورد نیاز برای وقوع یک واکنش و تبدیل مواد اولیه به محصولات. حالت گذار یک واسطه مولکولی بین ماده اولیه و محصول آن است. آنزیم سعی دارد که انرژی فعالسازی را کاهش داده و به سرعت فرایند کمک کند. در واکنش‌های آنزیمی، آنزیم با سوبسترا واکنش داده و پس از مرحله گذار، محصول یا پروداکت تولید می‌شود.

این همان فرض اولیه در کنتیک آنزیمی و مدلسازی دینامیکی است که بسیار ساده می‌باشد. یک سلول همیشه در یک حالت نیست و از حالتی به حالت دیگر تغییر می‌کند. انجام این فرایند به کمک تغییراتی که در مواد رخ می‌دهد امکان‌پذیر می‌شود، فرایندهایی که سلول را وارد شرایط دینامیکی و نه ایستا می‌کند.

مرحله محدود کننده سرعت هر واکنشی کندترین مرحله آن است و این همان چیزی است که سرعت کل واکنش را تعیین می‌کند. در واکنش‌های آنزیمی، تبدیل کمپلکس آنزیم- سوبسترا به محصول معمولاً محدود کننده سرعت است. سرعت این مرحله (و در نتیجه کل واکنش آنزیمی) به طور مستقیم با غلظت کمپلکس آنزیم- سوبسترا متناسب است. غلظت کمپلکس ES با پیشرفت واکنش تغییر می‌کند و بنابراین سرعت تشکیل محصول نیز بر این اساس تغییر می‌کند. هنگامی که واکنش به حالت تعادل می‌رسد (فاز حالت پایدار)، غلظت ES (و بنابراین سرعت واکنش) نسبتاً ثابت می‌ماند.

کینتیک Michaelis-Menten مدلی از کینتیک آنزیمی است که توضیح می‌دهد چگونه سرعت یک واکنش کاتالیز شده توسط آنزیم به غلظت آنزیم و سوبسترای آن بستگی دارد. بیایید واکنشی را در نظر بگیریم که در آن یک سوبسترا (S) به طور برگشت‌پذیر به یک آنزیم (E) متصل می‌شود و یک کمپلکس آنزیم-سوبسترا (ES) تشکیل می‌دهد، که سپس به‌طور برگشت‌ناپذیر واکنش داده تا یک محصول (P) را تشکیل دهد و دوباره آنزیم را آزاد کند.

S + E ⇌ ES → P + E

دو اصطلاح مهم در کینتیک Michaelis-Menten عبارتند از:

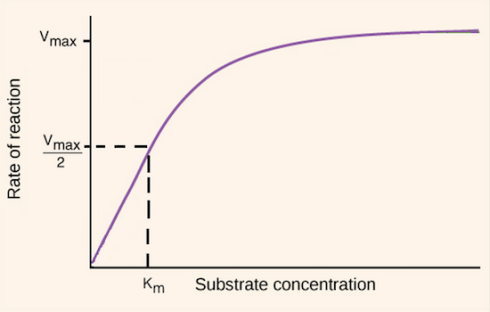
Vmax – حداکثر سرعت واکنش، زمانی که تمام مکان‌های فعال آنزیم با سوبسترا اشباع شده است.

Km (همچنین به عنوان ثابت Michaelis شناخته می‌شود) – غلظت سوبسترایی که در آن سرعت واکنش 50٪ Vmax است. Km معیاری از تمایل آنزیم به سوبسترای خود است، زیرا هرچه مقدار Km کمتر باشد، آنزیم در انجام عملکرد خود در غلظت کمتر کارآمدتر است.

استفاده از مدلسازی دینامیکی، که شامل اطلاعات جنبشی دقیق سیستم‌های بیولوژیکی است، به طور بالقوه دامنه کاربردها و دقت پیش‌بینی فنوتیپ را افزایش می‌دهد. تلاش‌های جدید در مهندسی متابولیک با هدف برطرف کردن شکاف بین این رویکرد و سایر پارادایم‌های مختلف مدل‌سازی ریاضی، به عنوان رویکردهای مبتنی بر اعمال قید است.

ابزارهای سیستم بیولوژی و بیوانفورماتیک به تجزیه و تحلیل داده‌ها و ویژگی‌های مرتبط (به عنوان مثال، توالی‌یابی ژنوم) در تحقیقات بیولوژیکی و زیست‌پزشکی برای ایجاد اکتشافات مبتنی بر مدل کمک می‌کنند. این امر علاقه به ساخت شبکه‌های در مقیاس ژنومی را ایجاد کرده است که امکان انجام شبیه‌سازی‌های کامپیوتری سیستم‌های بیولوژیکی پیچیده و درک نحوه تغییر توزیع‌های شار متابولیک در یک شبکه بیولوژیکی خاص برای پیش‌بینی فنوتیپ‌های سلولی را فراهم می‌کند.

علاوه بر این، مدلسازی دینامیکی و ریاضیاتی متابولیسم سلولی، که تحت شرایط مختلف محیطی و ژنتیکی مورد مطالعه قرار گرفته است، مهندسی متابولیک برای طراحی سویه‌های مطلوب، با انتخاب بهینه حذف‌های ژن برای تولید بیش از حد ترکیبات صنعتی را ممکن کرده است.

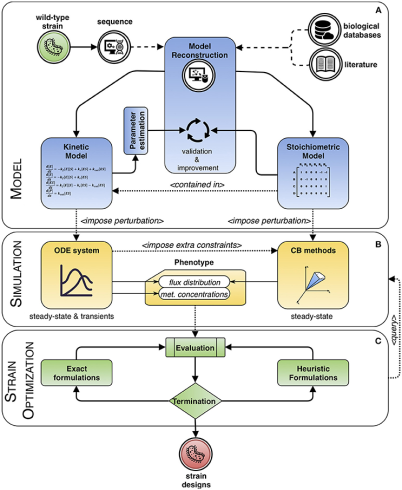
مدلسازی دینامیکی شبکه متابولیک می‌تواند مبتنی بر دانش کینتیک آنزیمی و داده‌های تجربی برای ساختن نمایشی از یک سیستم پویا باشد که قادر به توصیف تغییرات غلظت متابولیت‌ها در طول زمان با استفاده از سیستم‌های معادلات دیفرانسیل معمولی (ODE) است. این ODE ها حاوی مقادیر اولیه برای غلظت متابولیت، معادلات سرعت واکنش و پارامترهای جنبشی هستند. این نمایش‌ها برای مدل‌سازی مسیرهای متابولیک مرکزی در مقیاس کوچک ارگانیسم‌های شناخته‌شده، مانند ساکارومایسس سرویزیه و اشریشیا به کار گرفته شده است.

این چارچوب، که وظایف مدلسازی دینامیکی متابولیسم سلولی را با استفاده از یک فرمول مبتنی بر پویایی فرآیندهای متابولیک انجام می‌دهد، راه‌حل‌های دقیق و منحصربه‌فردی را در زمان برای حالت‌های گذرا و تعادل، از هر شرایط غلظت اولیه متابولیت ارائه می‌دهد. این رویکرد بر اساس قوانین سرعت جنبشی استنباط شده از اطلاعات بیوشیمیایی و مکانیکی است، در حالی که مقادیر شار نهایی مستقیماً از قوانین نرخ و غلظت متابولیت در حالت تعادل به دست می‌آیند.

با این حال، این نوع مدل‌سازی به مقادیر قابل‌توجهی از داده‌ها نیاز دارد که همیشه در دسترس نیستند، مانند پارامترهای جنبشی یا غلظت کل، و کار پارامترسازی برای مدل‌های بزرگ‌تر می‌تواند زمان‌بر و محاسباتی باشد.

در مقابل حالت پویا، یک جایگزین محدود کردن مدلسازی دینامیکی به گونه‌ای است که فقط استوکیومتری واکنش و برگشت‌پذیری را شامل شود که بر اساس فرض عملکرد حالت پایدار انجام می‌شود. بنابراین این روش قادر به بیان رفتارهای گذرا نیست.

در این رویکرد، مدل‌ها از فرمول‌بندی‌های مبتنی بر سیستم‌های معادلات خطی استفاده می‌کنند که معمولاً تعیین‌نشده هستند، یعنی تعداد معادلات بزرگ‌تر از تعداد متغیرها است که به تعداد بی‌نهایت راه‌حل ممکن ترجمه می‌شوند.

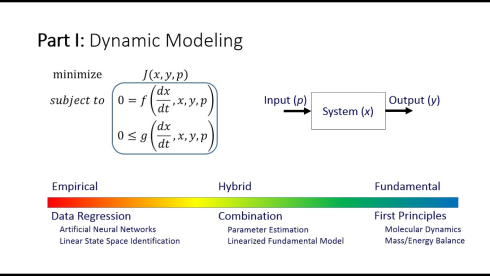
از مدل سازی ریاضی می توان برای توضیح یا پیش بینی رفتار یک سیستم استفاده کرد. در این شرایط برای بهینه‌سازی ما مجبور به استفاده از محدودیت‌ها یا قیود هستیم. این فرمول بر اساس استوکیومتری، از طریق مدل‌سازی مبتنی بر قید است که به تعریف محدودیت‌های رفتار یک سیستم بسته به محدودیت‌های فیزیکی و شیمیایی، مانند شار، تعادل جرم و ترمودینامیک کمک می‌کند.

این رویکرد راه‌حل‌هایی را به دست می‌دهد که ممکن است منحصربه‌فرد نباشند و به صورت توزیع‌های شار حالت پایدار نشان داده می‌شوند. بااین‌حال، روش‌های مدلسازی دینامیکی، تغییرات متابولیت‌ها و کینتیک آنزیمی را نیز در نظر می‌گیرند که این خود به درک بهتر سیستم‌های سلولی کمک می‌کند.

دوره کارآموزی طراحی و مدلسازی سلولی: سیستم بیولوژی